ZDoom

(317, 200)
(195, 100)
(98, 0)

if the following three points are on a curve, likely a parabola, and the rest of the line reflects this sort of change in rate... what would you call this, and, a question that's fairly old but huge - is there a formula to find other points on the line? normally, i can come up with formulas out of nowhere, but suddenly, i'm blank. the provided points were generated off of something i'm working on - but they're more of an example than anything. rather than an answer, i would strongly like to know - what is this, and how would one solve it? they are, of course, equidistant on the y-axis.

Oh my god, I haven't taken Trigonometry in over ten years. I think I need to brush up.

Yep. I have no clue. I am useless at math.

Isn't that a bezier curve?

kodi wrote:Isn't that a bezier curve?

that was one of the previous assumptions i had made; in this scenario, all three points are on the line, and represent the rate of curvature. it's almost comparable to exponential or logarithmic curves, or segments of them.

it's almost like, if one draws two lines out of a point; one goes straight up, and the other goes off to the side, but slowly curves upwards with the perfectly straight one; one could make two points at the same height on both lines, but the distance between these points would change at a certain rate, and finding this rate is my goal (i apologize for the kind of less-descriptive original post...)



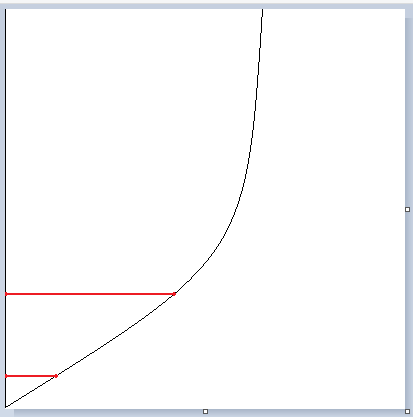
this is a quick illustration of the two lines scenario; if the difference in the x-values of these are combined with the y-values in the coordinates, it would form what i'm trying to describe (if that is, in fact, a bezier curve, it all goes to show that i really needed this thread
it's not a clean parabola, but i have little clue how to use the paint line tool with curves (it's also possible that i forgot exactly what shape to draw... )

Well the graph you drew looks more like something along the lines of
x + (x*0.02)^4 [or "x + (x*0.005)^8" for an even sharper spike]
Where the "go fucking nuts" exponential growth is delayed through making the number that is being raised in powers (me not good at math in english) progress slower through abusing a 0<n<1 multiplication.

Seemingly this is part of what people use for fast 3D graphics rendering when trying to make glossy materials have sharp light spread, since it's a neat approximation of a sudden spike in brightness.

I don't understand the question, since with three distinct and misaligned point you can generate an unique parabola and also an unique circumference...

Edward-san wrote:I don't understand the question, since with three distinct and misaligned point you can generate an unique parabola and also an unique circumference...

i blame my poor graphic... i meant parabolas in this case. one big element of the question is the fact that these points would all be on the line, as most of the formulas i find derive their curve or parabola from surrounding points. i don't have enough of a mathematical education to be extremely clear about it, but if this does seem like a question you'd be interested in answering, i could try to provide more information

Sorry, I'm a bit lost on the question. Anyways, by 'would all be on the line' do you mean the straight line or a curved line? There's quite a difference, because the points at the top post aren't on a straight line.

Let's call the points A = (317, 200), B = (195, 100) and C = (98, 0). If you calculate the slope of AB and BC, they don't match.

Slope formula:
mAB = (200-100)/(317-195) = 100/122
mBC = (100-0)/(195-98) = 100/97